Chapter 2: Visualization of functions
Figure 1
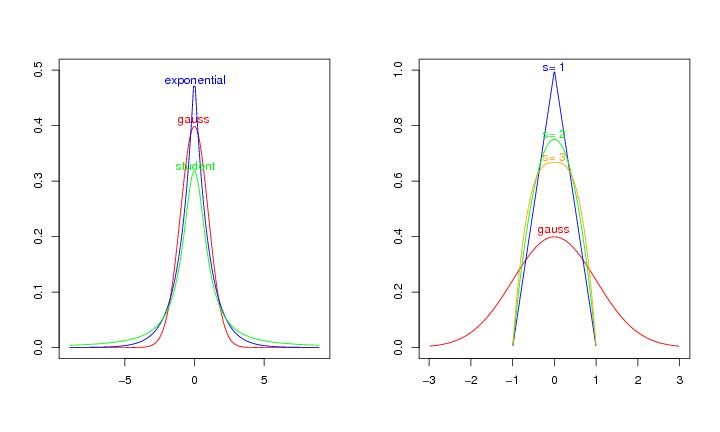
N<-150
pnum<-N
# frame 1
lift<-0.01
colot<-c("red","blue","green","orange")
type<-c("gauss","exponential","student")
xmax<-9
support<-c(-xmax,xmax)
ymax<-0.5
plot(x="",y="",xlim=c(-xmax,xmax),ylim=c(0,ymax),xlab="",ylab="")
for (i in 1:length(type)){
func<-type[i]
col<-colot[i]
pcf<-eval.func.1D(func,N,support=support)
dp<-draw.pcf(pcf,pnum=pnum)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-which.max(dp$y);text(dp$x[inde],dp$y[inde]+lift,func,col=col)
}
# frame 2
# gauss
lift<-0.02
xmax<-3
ymax<-1
plot(x="",y="",xlim=c(-xmax,xmax),ylim=c(0,ymax),xlab="",ylab="")
func<-"gauss"
col<-"red"
support<-c(-xmax,xmax)
pcf<-eval.func.1D(func,N,support=support)
dp<-draw.pcf(pcf,pnum=pnum)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-which.max(dp$y);text(dp$x[inde],dp$y[inde]+lift,"gauss",col=col)
# polynomial
func<-"polynomial"
g<-1
col<-"blue"
pcf<-eval.func.1D(func,N,support=support,g=g)
dp<-draw.pcf(pcf,pnum=pnum)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-which.max(dp$y);text(dp$x[inde],dp$y[inde]+lift,
paste("s=",as.character(g)),col=col)
g<-2
col<-"green"
pcf<-eval.func.1D(func,N,support=support,g=g)
dp<-draw.pcf(pcf,pnum=pnum)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-which.max(dp$y);text(dp$x[inde],dp$y[inde]+lift,
paste("s=",as.character(g)),col=col)
g<-3
col<-"orange"
pcf<-eval.func.1D(func,N,support=support,g=g)
dp<-draw.pcf(pcf,pnum=pnum)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-which.max(dp$y);text(dp$x[inde],dp$y[inde]+lift,
paste("s=",as.character(g)),col=col)
Figure 2
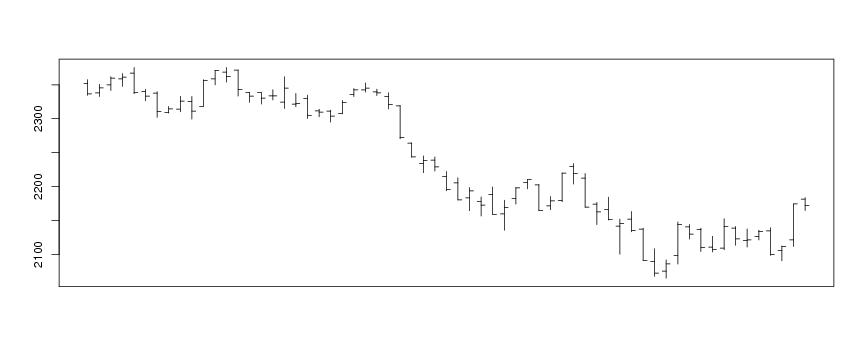
# download the file barchart.txt
file<-"~/barchart.txt"
datamat<-read.table(file=file)
dendat<-datamat[,1]
low<-datamat[,2]
high<-datamat[,3]
open<-datamat[,4]
aika<-seq(1:length(dendat))
xmin<-1
xmax<-length(dendat)
ymin<-min(low)
ymax<-max(high)
# frame
plot(x="",y="",type="n",ylim=c(ymin,ymax),xlab="",ylab="",xlim=c(xmin,xmax),
xaxt='n')
minnu<-1
vecpit<-minnu/3
x0<-aika-vecpit
y0<-open
x1<-aika
y1<-open
segments(x0,y0,x1,y1)
x0<-aika+vecpit
y0<-dendat
x1<-aika
y1<-dendat
segments(x0,y0,x1,y1)
x0<-aika
y0<-low
x1<-aika
y1<-high
segments(x0,y0,x1,y1)
Figure 3
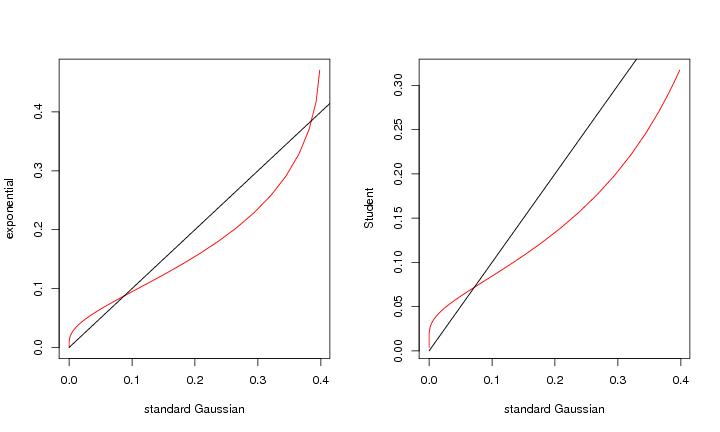
N<-150
pnum<-N
xmax<-9; support<-c(-xmax,xmax)
func<-"gauss"
pcf<-eval.func.1D(func,N,support=support)
dp<-draw.pcf(pcf,pnum=pnum)
func<-"exponential"
pcf<-eval.func.1D(func,N,support=support)
dp2<-draw.pcf(pcf,pnum=pnum)
func<-"student"
pcf<-eval.func.1D(func,N,support=support)
dp3<-draw.pcf(pcf,pnum=pnum)
# frame 1
plot(dp$y,dp2$y,type="l",ylab="exponential",xlab="standard Gaussian",col="red")
ma<-max(dp$y,dp2$y)
segments(0,0,ma,ma)
# frame 2
plot(dp$y,dp3$y,type="l",ylab="Student",xlab="standard Gaussian",col="red")
ma<-max(dp$y,dp3$y)
segments(0,0,ma,ma)
Figure 4
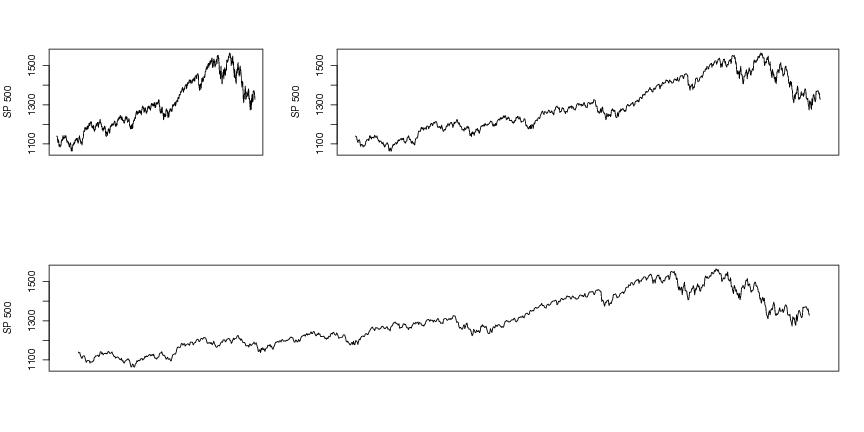
# download the file aspect.txt
file<-"~/aspect.txt"
dendat<-read.table(file=file)
# frames
layout(matrix(c(1,2,3,3), 2, 2, byrow = TRUE),widths=c(1,2,3))
plot(dendat[,1],type="l",xlab="",ylab="SP 500",xaxt="n")
plot(dendat[,1],type="l",xlab="",ylab="SP 500",xaxt="n")
plot(dendat[,1],type="l",xlab="",ylab="SP 500",xaxt="n")
Figure 5
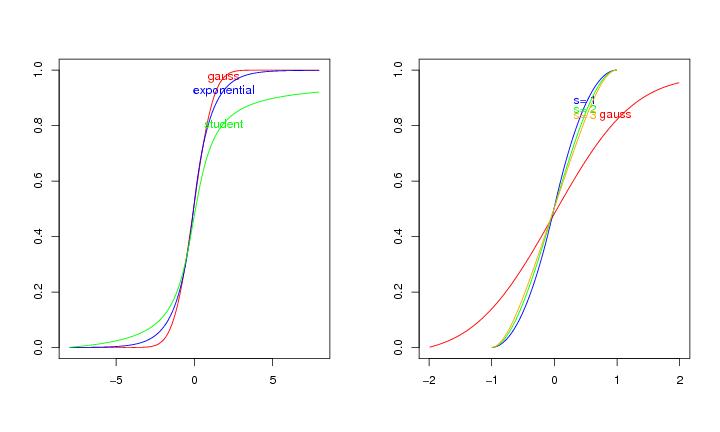
N<-150
pnum<-N
# frame 1
colot<-c("red","blue","green","orange")
type<-c("gauss","exponential","student")
xmax<-8
support<-c(-xmax,xmax)
ymax<-1
plot(x="",y="",xlim=c(-xmax,xmax),ylim=c(0,1),xlab="",ylab="")
for (i in 1:length(type)){
func<-type[i]
col<-colot[i]
pcf<-eval.func.1D(func,N,support=support,distr=TRUE)
dp<-draw.pcf(pcf,pnum=pnum) #,dens=FALSE)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-floor(2.5*N/4);text(dp$x[inde],dp$y[inde],func,col=col)
}
# frame 2
lift<-0.02
fac<-0.75
xmax<-2
support<-c(-xmax,xmax)
plot(x="",y="",xlim=c(-xmax,xmax),ylim=c(0,1),xlab="",ylab="")
func<-"gauss"
col<-"red"
pcf<-eval.func.1D(func,N,support=support,distr=TRUE)
dp<-draw.pcf(pcf,pnum=pnum)#,dens=FALSE)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-floor(fac*N);text(dp$x[inde],dp$y[inde]+lift,"gauss",col=col)
func<-"polynomial"
g<-1
col<-"blue"
pcf<-eval.func.1D(func,N,support=support,g=g,distr=TRUE)
dp<-draw.pcf(pcf,pnum=pnum)#,dens=FALSE)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-floor(fac*N);text(dp$x[inde],dp$y[inde]+lift,
paste("s=",as.character(g)),col=col)
g<-2
col<-"green"
pcf<-eval.func.1D(func,N,support=support,g=g,distr=TRUE)
dp<-draw.pcf(pcf,pnum=pnum)#,dens=FALSE)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-floor(fac*N);text(dp$x[inde],dp$y[inde]+lift,
paste("s=",as.character(g)),col=col)
g<-3
col<-"orange"
pcf<-eval.func.1D(func,N,support=support,g=g,distr=TRUE)
dp<-draw.pcf(pcf,pnum=pnum)#,dens=FALSE)
matpoints(dp$x,dp$y,type="l",xlab="",ylab="",col=col)
inde<-floor(fac*N);text(dp$x[inde],dp$y[inde]+lift,
paste("s=",as.character(g)),col=col)
Figure 6
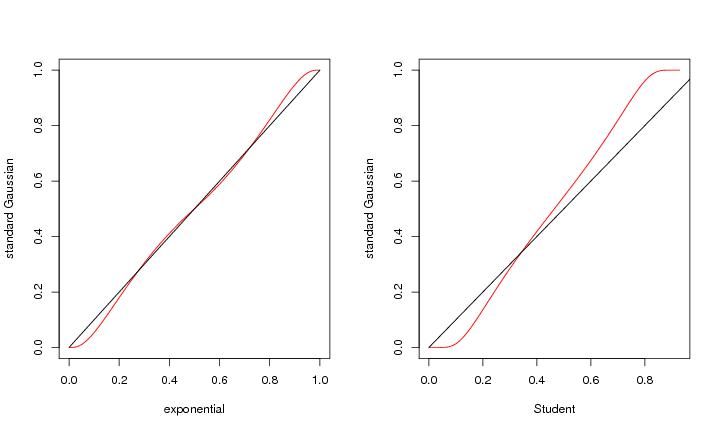
N<-150
pnum<-N
xmax<-9; support<-c(-xmax,xmax)
func<-"gauss"
pcf<-eval.func.1D(func,N,support=support,distr=TRUE)
dp<-draw.pcf(pcf,pnum=pnum)
func<-"exponential"
pcf<-eval.func.1D(func,N,support=support,distr=TRUE)
dp2<-draw.pcf(pcf,pnum=pnum)
func<-"student"
pcf<-eval.func.1D(func,N,support=support,distr=TRUE)
dp3<-draw.pcf(pcf,pnum=pnum)
# frame 1
plot(dp2$y,dp$y,type="l",xlab="exponential",ylab="standard Gaussian",col="red")
ma<-max(dp$y,dp2$y)
segments(0,0,ma,ma)
# frame 2
plot(dp3$y,dp$y,type="l",xlab="Student",ylab="standard Gaussian",col="red")
ma<-max(dp$y,dp3$y)
segments(0,0,ma,ma)
Figure 7
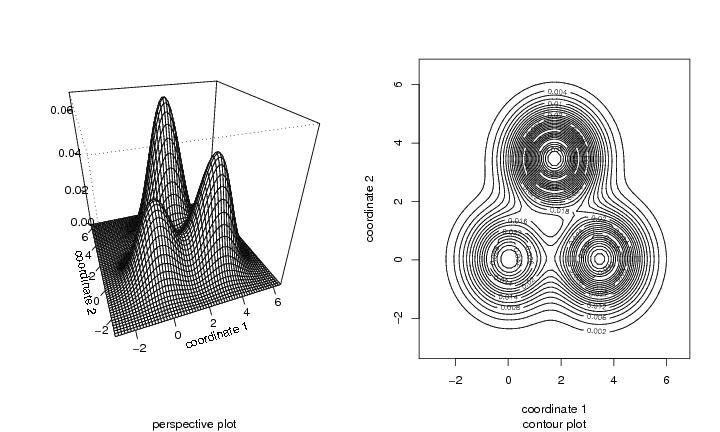
N<-c(60,60)
pcf<-sim.data(N=N,type="mulmod")
dp<-draw.pcf(pcf)
# left frame
persp(x=dp$x,y=dp$y,z=dp$z,
xlab="coordinate 1",ylab="coordinate 2",zlab="",
ticktype="detailed",
phi=30,theta=-20)
title(sub="perspective plot")
# right frame
contour(dp$x,dp$y,dp$z,
xlab="coordinate 1",ylab="coordinate 2",
nlevels=25)
title(sub="contour plot")
Figure 8
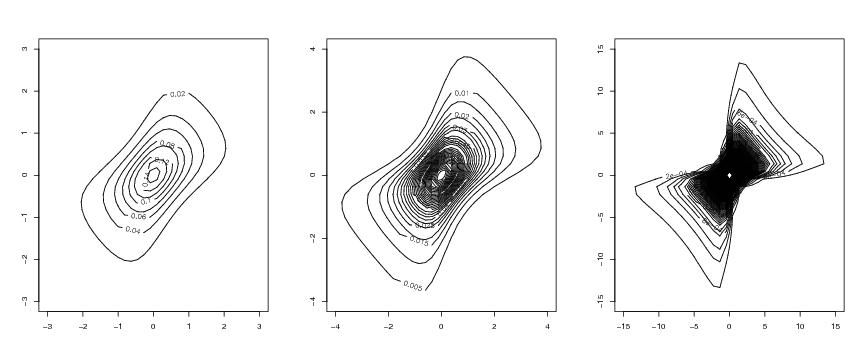
func<-"gauss"
N<-c(32,32)
marginal<-"student"
r<-0.8
t<-1
nlev<-c(10,50,500)
supo<-c(3,4,15)
# frame 1
i<-1
nlevel<-nlev[i]
yla<-supo[i]
ala<--yla
support<-c(ala,yla,ala,yla)
ef<-pcf.func(func,N,t=c(t,t),support=support,marginal=marginal,r=r)
dp<-draw.pcf(ef)
contour(dp$x,dp$y,dp$z,nlevel=nlevel)
# frame 2
i<-2
nlevel<-nlev[i]
yla<-supo[i]
ala<--yla
support<-c(ala,yla,ala,yla)
ef<-pcf.func(func,N,t=c(t,t),support=support,marginal=marginal,r=r)
dp<-draw.pcf(ef)
contour(dp$x,dp$y,dp$z,nlevel=nlevel)
# frame 3
i<-3
nlevel<-nlev[i]
yla<-supo[i]
ala<--yla
support<-c(ala,yla,ala,yla)
ef<-pcf.func(func,N,t=c(t,t),support=support,marginal=marginal,r=r)
dp<-draw.pcf(ef)
contour(dp$x,dp$y,dp$z,nlevel=nlevel)
Figure 9
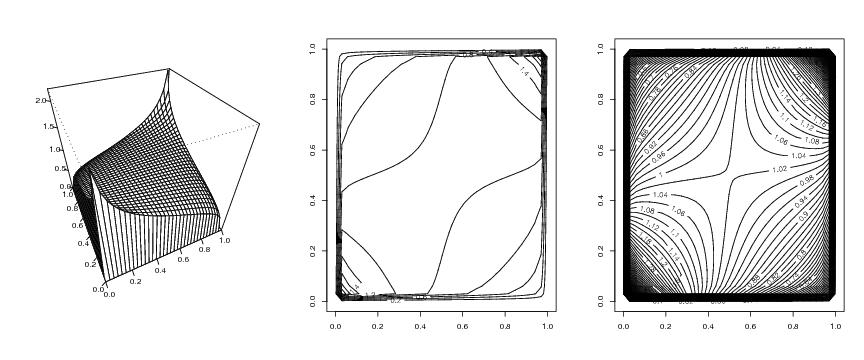
func<-"gauss"
N<-c(32,32)
marginal<-"unif"
r<-0.2
ef<-pcf.func(func,N,marginal=marginal,r=r)
dp<-draw.pcf(ef)
# frame 1
persp(dp$x,dp$y,dp$z,theta=-25,phi=40,ticktype="detailed",
xlab="",ylab="",zlab="")
# frame 2
contour(dp$x,dp$y,dp$z,xlab="",ylab="",nlevels=10)
# frame 3
contour(dp$x,dp$y,dp$z,xlab="",ylab="",nlevels=100)
Figure 10
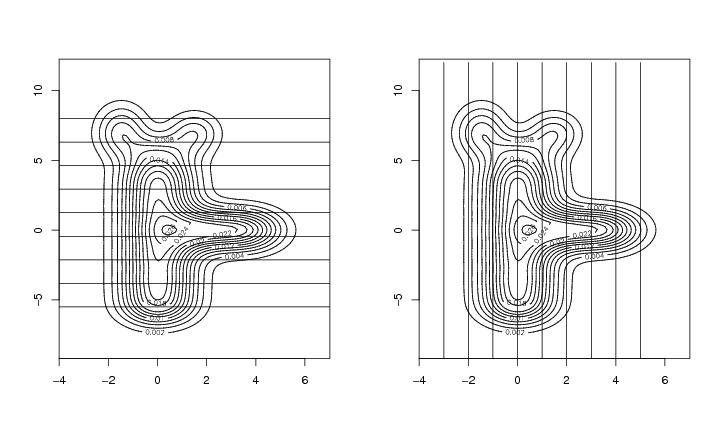
N<-c(100,100)
et<-sim.data(N=N,type="fox")
luk<-100
dm<-draw.pcf(et,pnum=c(luk,luk))
# Slices parallel to the x-axis
d1<-1
slicenum<-9
alaY<--5.5 #et$support[2*d1-1]
ylaY<-8 #et$support[2*d1]
hop<-(ylaY-alaY)/(slicenum-1)
gridiX<-seq(alaY,ylaY,hop)
# slices parallel to the y-axis
d1<-2
slicenum<-9
alaX<--3 #et$support[2*d1-1]
ylaX<-5 #et$support[2*d1]
hop<-(ylaX-alaX)/(slicenum-1)
gridiY<-seq(alaX,ylaX,hop)
# frame 1
contour(dm$x,dm$y,dm$z,nlevels=20)
for (i in 1:length(gridiX)) lines(c(-7,9.5),c(gridiX[i],gridiX[i]))
# frame 2
contour(dm$x,dm$y,dm$z,nlevels=20)
for (i in 1:length(gridiX)) lines(c(gridiY[i],gridiY[i]),c(-10,12))
Figure 11
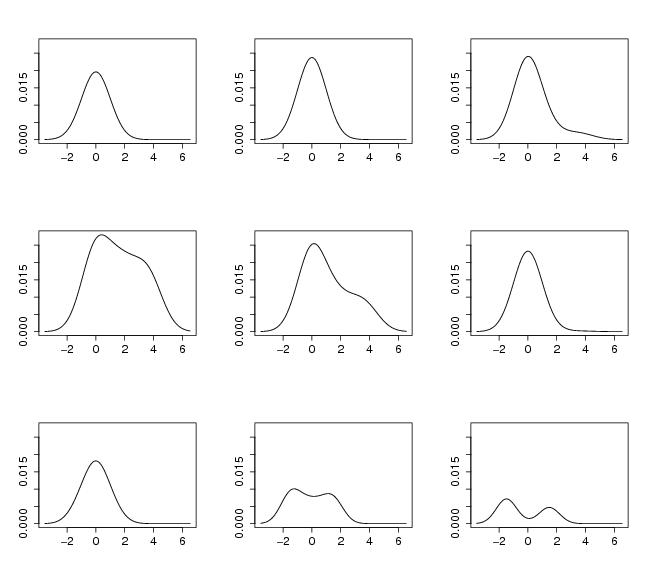
N<-c(100,100)
et<-sim.data(N=N,type="fox")
luk<-100
dm<-draw.pcf(et,pnum=c(luk,luk))
# Slices parallel to the x-axis
d1<-1
slicenum<-9
alaY<--5.5 #et$support[2*d1-1]
ylaY<-8 #et$support[2*d1]
hop<-(ylaY-alaY)/(slicenum-1)
gridiX<-seq(alaY,ylaY,hop)
maxi<-0
for (i in 1:length(gridiX)){
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
maxi<-max(sl$value,maxi)
}
# frame 1
i<-1
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 2
i<-2
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 3
i<-3
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 4
i<-4
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 5
i<-5
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 6
i<-6
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 7
i<-7
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 8
i<-8
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 9
i<-9
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
Figure 12

N<-c(100,100)
et<-sim.data(N=N,type="fox")
luk<-100
dm<-draw.pcf(et,pnum=c(luk,luk))
# slices parallel to the y-axis
d1<-2
slicenum<-9
alaX<--3 #et$support[2*d1-1]
ylaX<-5 #et$support[2*d1]
hop<-(ylaX-alaX)/(slicenum-1)
gridiY<-seq(alaX,ylaX,hop)
maxi<-0
for (i in 1:length(gridiY)){
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
maxi<-max(sl$value,maxi)
}
# frame 1
i<-1
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 2
i<-2
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 3
i<-3
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 4
i<-4
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 5
i<-5
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 6
i<-6
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 7
i<-7
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 8
i<-8
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 9
i<-9
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
Figure 13
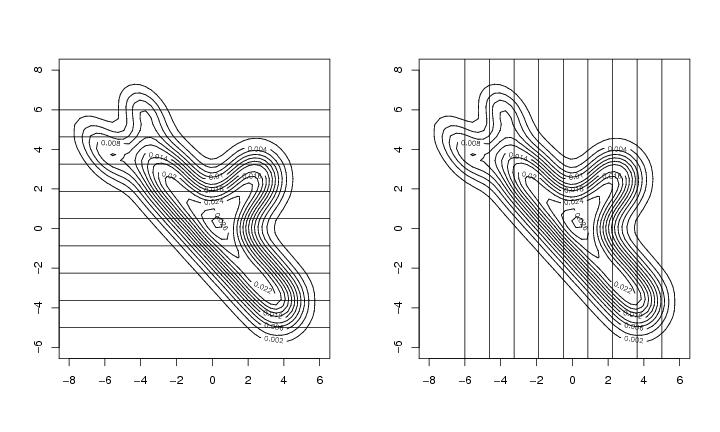
param<-sim.fox()
sig<-param$sig
M<-param$M
p<-param$p
N<-c(45,45)
theta<-pi/4
support<-c(-8,6,-6,8)
et<-pcf.func("mixt",N,sig=sig,M=M,p=p,theta=theta,support=support)
dm<-draw.pcf(et,pnum=c(60,60))
# Slices parallel to the x-axis
d1<-1
slicenum<-9
alaY<--5 #et$support[2*d1-1]
ylaY<-6 #et$support[2*d1]
hop<-(ylaY-alaY)/(slicenum-1)
gridiX<-seq(alaY,ylaY,hop)
# slices parallel to the y-axis
d1<-2
slicenum<-9
alaX<--6 #et$support[2*d1-1]
ylaX<-5 #et$support[2*d1]
hop<-(ylaX-alaX)/(slicenum-1)
gridiY<-seq(alaX,ylaX,hop)
# frame 1
contour(dm$x,dm$y,dm$z,nlevels=20)
for (i in 1:length(gridiX)) lines(c(-9,9.5),c(gridiX[i],gridiX[i]))
# frame 2
contour(dm$x,dm$y,dm$z,nlevels=20)
for (i in 1:length(gridiX)) lines(c(gridiY[i],gridiY[i]),c(-10,12))
Figure 14
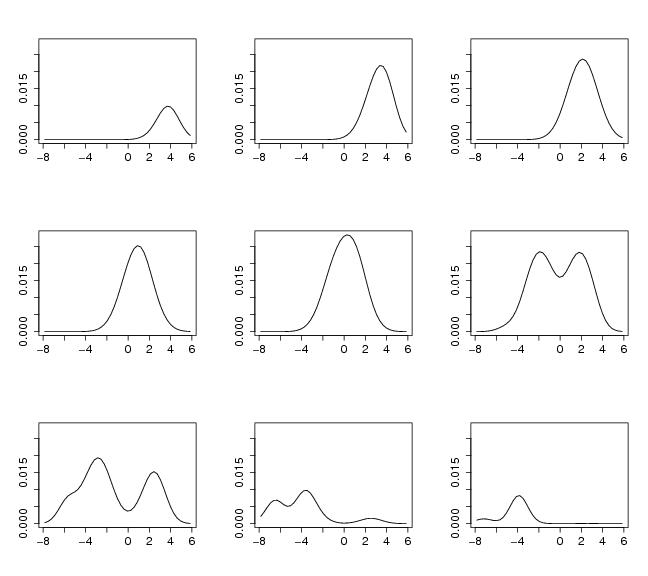
param<-sim.fox()
sig<-param$sig
M<-param$M
p<-param$p
N<-c(45,45)
theta<-pi/4
support<-c(-8,6,-6,8)
et<-pcf.func("mixt",N,sig=sig,M=M,p=p,theta=theta,support=support)
dm<-draw.pcf(et,pnum=c(60,60))
# Slices parallel to the x-axis
d1<-1
slicenum<-9
alaY<--5 #et$support[2*d1-1]
ylaY<-6 #et$support[2*d1]
hop<-(ylaY-alaY)/(slicenum-1)
gridiX<-seq(alaY,ylaY,hop)
maxi<-0
for (i in 1:length(gridiX)){
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
maxi<-max(sl$value,maxi)
}
# frame 1
i<-1
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 2
i<-2
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 3
i<-3
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 4
i<-4
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 5
i<-5
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 6
i<-6
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 7
i<-7
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 8
i<-8
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 9
i<-9
vecci<-gridiX[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
Figure 15
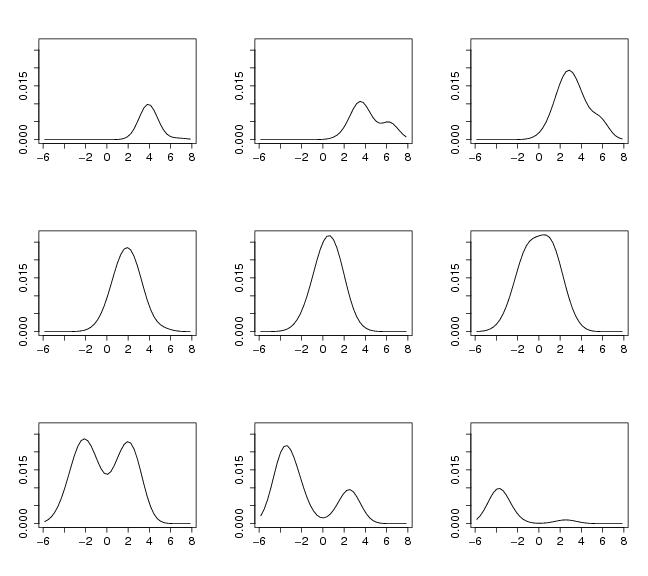
param<-sim.fox()
sig<-param$sig
M<-param$M
p<-param$p
N<-c(45,45)
theta<-pi/4
support<-c(-8,6,-6,8)
et<-pcf.func("mixt",N,sig=sig,M=M,p=p,theta=theta,support=support)
dm<-draw.pcf(et,pnum=c(60,60))
# slices parallel to the y-axis
d1<-2
slicenum<-9
alaX<--6 #et$support[2*d1-1]
ylaX<-5 #et$support[2*d1]
hop<-(ylaX-alaX)/(slicenum-1)
gridiY<-seq(alaX,ylaX,hop)
maxi<-0
for (i in 1:length(gridiY)){
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
maxi<-max(sl$value,maxi)
}
# frame 1
i<-1
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 2
i<-2
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 3
i<-3
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 4
i<-4
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 5
i<-5
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 6
i<-6
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 7
i<-7
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 8
i<-8
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
# frame 9
i<-9
vecci<-gridiY[i]
sl<-slicing(et,vecci,d1=d1)
dms<-draw.pcf(sl)
plot(dms$x,dms$y,type="l",xlab="",ylab="",ylim=c(0,maxi),cex.axis=1.5)
Figure 16

param<-sim.fox()
sig<-param$sig
M<-param$M
p<-param$p
supportx<-c(-4,8)
supporty<-c(-10,11)
# frame 1
# projection to x-axis
Mx<-M[,1]
sigx<-sig[,1]
N<-100
et<-pcf.func(func="mixt",M=Mx,sig=sigx,p=p,N=N,support=supportx)
dm<-draw.pcf(et)
plot(dm$x,dm$y,type="l",xlab="",ylab="")
# frame 2
# projection to y-axis
My<-M[,2]
sigy<-sig[,2]
et<-pcf.func(func="mixt",M=My,sig=sigy,p=p,N=N,support=supporty)
dm<-draw.pcf(et)
plot(dm$x,dm$y,type="l",xlab="",ylab="")
Figure 17
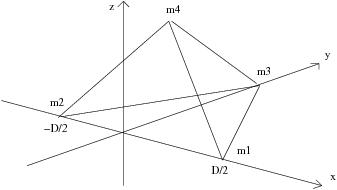
Figure 18

d<-3
dproj<-2
dist<-3
height<-sqrt(3)/2 # sqrt(3)/2 = 0.8660254
len<-1/(2*sqrt(3)) # 1/(2*sqrt(3)) = 0.2886751
kor<-sqrt(2/3) # sqrt(2/3) = 0.8164966
moodi<-4
sig<-matrix(1,moodi,dproj)
p<-rep(1,moodi)/moodi
# Projection to x-y plane.
Mxy<-matrix(0,moodi,dproj)
Mxy[1,]<-dist*c(1/2,0)
Mxy[2,]<-dist*c(-1/2,0)
Mxy[3,]<-dist*c(0,height)
Mxy[4,]<-dist*c(0,len)
N<-c(60,60)
M<-Mxy
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p) #dmxy<-drawmix(Mxy,sig,p,plkm=60)
dmxy<-draw.pcf(pcf,pnum=N)
# Projection to x-z plane.
Mxz<-matrix(0,moodi,dproj)
Mxz[1,]<-dist*c(1/2,0)
Mxz[2,]<-dist*c(-1/2,0)
Mxz[3,]<-dist*c(0,0)
Mxz[4,]<-dist*c(0,kor)
#dmxz<-drawmix(Mxz,sig,p,plkm=60)
N<-c(60,60)
M<-Mxz
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p) #dmxy<-drawmix(Mxy,sig,p,plkm=60)
dmxz<-draw.pcf(pcf,pnum=N)
# Projection to y-z plane.
Myz<-matrix(0,moodi,dproj)
Myz[1,]<-dist*c(0,0)
Myz[2,]<-dist*c(0,0)
Myz[3,]<-dist*c(height,0)
Myz[4,]<-dist*c(len,kor)
N<-c(60,60)
M<-Myz
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p) #dmxy<-drawmix(Mxy,sig,p,plkm=60)
dmyz<-draw.pcf(pcf,pnum=N)
# bigger distance
dist<-4
Mxy<-matrix(0,moodi,dproj)
Mxy[1,]<-dist*c(1/2,0)
Mxy[2,]<-dist*c(-1/2,0)
Mxy[3,]<-dist*c(0,height)
Mxy[4,]<-dist*c(0,len)
N<-c(60,60)
M<-Mxy
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p) #dmxy<-drawmix(Mxy,sig,p,plkm=60)
dm<-draw.pcf(pcf,pnum=N)
# frame 1
persp(dmxy$x,dmxy$y,dmxy$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"(a)",cex=1.5)
# frame 2
persp(dmxz$x,dmxz$y,dmxz$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"(b)",cex=1.5)
# frame 3
persp(dmyz$x,dmyz$y,dmyz$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"(c)",cex=1.5)
# frame 4
persp(dm$x,dm$y,dm$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"(d)",cex=1.5)
Figure 19

dist<-4 # determines the distance between vertices of the pentahedron
d<-4
moodi<-5
M<-matrix(0,moodi,d)
M[1,]<-dist*c(1/2, 0,0,0)
M[2,]<-dist*c(-1/2,0,0,0)
M[3,]<-dist*c(0,sqrt(3)/2,0,0)
M[4,]<-dist*c(0,1/(2*sqrt(3)),sqrt(2/3),0)
M[5,]<-dist*c(0,1/(2*sqrt(3)),1/(2*sqrt(6)),sqrt(15/24))
sig<-matrix(1,moodi,d)
p0<-1/moodi
p<-p0*rep(1,moodi)
dist<-4
dproj<-2
sig<-matrix(1,moodi,dproj)
# Projection to x-y plane.
M<-matrix(0,moodi,dproj)
M[1,]<-dist*c(1/2,0)
M[2,]<-dist*c(-1/2,0)
M[3,]<-dist*c(0,sqrt(3)/2)
M[4,]<-dist*c(0,1/(2*sqrt(3)))
M[5,]<-dist*c(0,1/(2*sqrt(3)))
N<-c(60,60)
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p)
dmxy<-draw.pcf(pcf,pnum=N)
# Projection to x-z plane.
M<-matrix(0,moodi,dproj)
M[1,]<-dist*c(1/2,0)
M[2,]<-dist*c(-1/2,0)
M[3,]<-dist*c(0,0)
M[4,]<-dist*c(0,sqrt(2/3))
M[5,]<-dist*c(0,1/(2*sqrt(6)))
N<-c(60,60)
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p)
dmxz<-draw.pcf(pcf,pnum=N)
# Projection to x-u plane.
M<-matrix(0,moodi,dproj)
M[1,]<-dist*c(1/2,0)
M[2,]<-dist*c(-1/2,0)
M[3,]<-dist*c(0,0)
M[4,]<-dist*c(0,0)
M[5,]<-dist*c(0,sqrt(15/24))
N<-c(60,60)
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p) #dmxy<-drawmix(Mxy,sig,p,plkm=60)
dmxu<-draw.pcf(pcf,pnum=N)
# Projection to y-z plane.
M<-matrix(0,moodi,dproj)
M[1,]<-dist*c(0,0)
M[2,]<-dist*c(0,0)
M[3,]<-dist*c(sqrt(3)/2,0)
M[4,]<-dist*c(1/(2*sqrt(3)),sqrt(2/3))
M[5,]<-dist*c(1/(2*sqrt(3)),1/(2*sqrt(6)))
N<-c(60,60)
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p)
dmyz<-draw.pcf(pcf,pnum=N)
# Projection to y-u plane.
M<-matrix(0,moodi,dproj)
M[1,]<-dist*c(0,0)
M[2,]<-dist*c(0,0)
M[3,]<-dist*c(sqrt(3)/2,0)
M[4,]<-dist*c(1/(2*sqrt(3)),0)
M[5,]<-dist*c(1/(2*sqrt(3)),sqrt(15/24))
N<-c(60,60)
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p)
dmyu<-draw.pcf(pcf,pnum=N)
# Projection to z-u plane.
M<-matrix(0,moodi,dproj)
M[1,]<-dist*c(0,0)
M[2,]<-dist*c(0,0)
M[3,]<-dist*c(0,0)
M[4,]<-dist*c(sqrt(2/3),0)
M[5,]<-dist*c(1/(2*sqrt(6)),sqrt(15/24))
N<-c(60,60)
pcf<-pcf.func("mixt",N,sig=sig,M=M,p=p)
dmzu<-draw.pcf(pcf,pnum=N)
# frame 1
persp(dmxy$x,dmxy$y,dmxy$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"a)",cex=1.5)
# frame 2
persp(dmxz$x,dmxz$y,dmxz$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"b)",cex=1.5)
# frame 3
persp(dmxu$x,dmxu$y,dmxu$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"c)",cex=1.5)
# frame 4
persp(dmyz$x,dmyz$y,dmyz$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"d)",cex=1.5)
# frame 5
persp(dmyu$x,dmyu$y,dmyu$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"e)",cex=1.5)
# frame 6
persp(dmzu$x,dmzu$y,dmzu$z,phi=30,theta=130,box=FALSE,col="white")
text(-0.3,-0.4,"f)",cex=1.5)
Figure 20

volball<-function(r,d){ return(r^d*pi^(d/2)/gamma(d/2+1)) }
volsphere<-function(d){ return(2*pi^(d/2)/gamma(d/2)) }
maksimit<-function(d,type,sig=1,nu=1)
{
if (type=="gauss"){
maksi<-(2*pi)^(-d/2)
}
if (type=="bartlett"){
maksi<-sig^{-d}*(volsphere(d)*2/(d*(d+2)))^(-1)
}
if (type=="student"){
maksi<-gamma((nu+d)/2)/(gamma(nu/2)*(pi*nu)^(d/2))
}
if (type=="bartlett2"){
maksi<-(volsphere(d)*2^(1-d)/(d*(d+2)))^(-1)
}
return(maksi)
}
voluumit<-function(d,leve,type,sig=1,nu=1)
{
if (type=="gauss"){
norma<-(2*pi)^{-d/2}
radi<-sig*sqrt(-2*log(leve*sig^d/norma)) #sig*sqrt(-2*log(leve)-d*log(2*pi))
}
if (type=="bartlett"){
norma<-d*(d+2)/(2*volsphere(d))
radi<-sig*sqrt(1-leve*sig^d/norma)
#maksi<-sig^{-d}*(volsphere(d)*2/(d*(d+2)))^(-1)
#radi<-sig*sqrt(1-leve/maksi)
}
if (type=="student"){
norma<-gamma((nu+d)/2)/(gamma(nu/2)*(pi*nu)^(d/2))
radi<-nu*(exp(-2*log(leve/norma)/(d+nu))-1)
}
if (type=="bartlett2"){
maksi<-(volsphere(d)*2^(1-d)/(d*(d+2)))^(-1)
radi<-sqrt(1-leve/maksi)/2
}
volu<-volball(radi,d)
return(list(volu=volu,radi=radi))
}
volugene<-function(d,lnum,type,epsi=NULL,sig=1,nu=1)
{
maksi<-maksimit(d,type,sig=sig,nu=nu)
if (is.null(epsi)){
step<-maksi/(lnum)
minni<-step
}
else{
minni<-epsi
step<-(maksi-minni)/lnum
}
levels<-seq(minni,(maksi),step)
maksivol<-voluumit(d,levels[1],type,sig=sig,nu=nu)$volu
x<-matrix(0,2*lnum,1)
y<-matrix(0,2*lnum,1)
x[1]<-0
x[2*lnum]<-maksivol
y[1]<-levels[1]
y[2*lnum]<-y[1]
for (i in 2:(lnum-1)){
volpre<-voluumit(d,levels[i-1],type,sig=sig,nu=nu)$volu
volnyk<-voluumit(d,levels[i],type,sig=sig,nu=nu)$volu
erotus<-volpre-volnyk
x[i]<-x[i-1]+erotus/2
x[2*lnum-i+1]<-x[2*lnum-i+2]-erotus/2
y[i]<-levels[i]
y[2*lnum-i+1]<-y[i]
}
x[lnum]<-maksivol/2
x[lnum+1]<-maksivol/2
y[lnum]<-levels[lnum]
y[lnum+1]<-levels[lnum]
return(list(x=x,y=y)) #plot(x,y,type="l")
}
d<-1
type<-"bartlett"
sig<-1
mak<-maksimit(d,type,sig=sig)
lkm<-100
step<-mak/lkm
leve<-seq(step,mak-step,step)
vol<-voluumit(d,leve,type,sig=sig)
vg<-volugene(d,lnum=1000,type=type,sig=sig)
# frame 1
plot(leve,vol$volu,type="l",xlab="level",ylab="volume")
# frame 2
plot(vol$volu,leve,type="l",xlab="volume",ylab="level")
# frame 3
plot(vg$x,vg$y,type="l",xlab="volume",ylab="level")
Figure 21
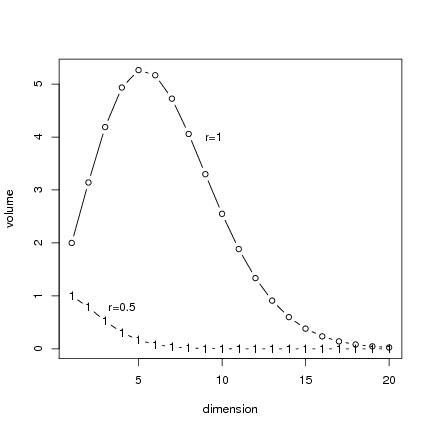
dime<-seq(1,20,1)
r<-1/2
eka<-volball(r,dime)
r<-1
toka<-volball(r,dime)
# frame
plot(dime,toka,type="b",xlab="dimension",ylab="volume")
matpoints(dime,eka,type="b")
text(9.5,4,"r=1")
text(4,0.8,"r=0.5")
Figure 22
plotunivol<-function(R,dimet,type,gnum=1000,sig=1,nu=1,inde=round(gnum/2))
{
xmax<-0
ymax<-0
for (i in 1:length(dimet)){
d<-dimet[i]
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=nu)
x<-rp$volu
y<-rp$level
xmax<-max(xmax,x)
ymax<-max(ymax,y)
}
plot(x="",y="",xlim=c(0,xmax),ylim=c(0,ymax),xlab="volume",ylab="level")
for (i in 1:length(dimet)){
d<-dimet[i]
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=nu)
x<-rp$volu
y<-rp$level
sy<-symme(x,y)
xp<-sy$x/2
yp<-sy$y
matpoints(xp,yp,type="l",xlab="volume",ylab="level")
text(xp[inde],yp[inde],paste("d=",as.character(dimet[i])))
}
}
symme<-function(x,y)
{
x11<-x[length(x)]-x
x1<-x11[length(x11):1]
x2<-x+x[length(x)]
x3<-c(x1,x2)
y1<-y[length(y):1]
y3<-c(y1,y)
return(list(x=x3,y=y3))
}
# frame 1
type<-"bartlett"
gnum<-1000
sig<-1
R<-1
dimet<-c(1,3,5,7,9)
plotunivol(R,dimet,type,gnum=gnum,inde=700)
# frame 2
sig<-1/2
R<-1/2
dimet<-c(1,3,5)
plotunivol(R,dimet,type,gnum=gnum,sig=sig,nu=nu,inde=700)
# frame 3
type<-"gauss"
gnum<-1000
sig<-1
R<-5
dimet<-c(1:2)
plotunivol(R,dimet,type,gnum=gnum,inde=700)
# frame 4
type<-"student"
nu<-1
R<-10
dimet<-c(1:2)
plotunivol(R,dimet,type,gnum=gnum,inde=700,nu=nu)
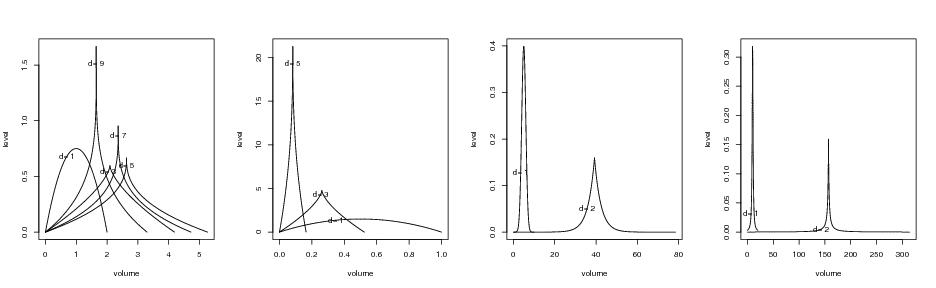
Figure 23
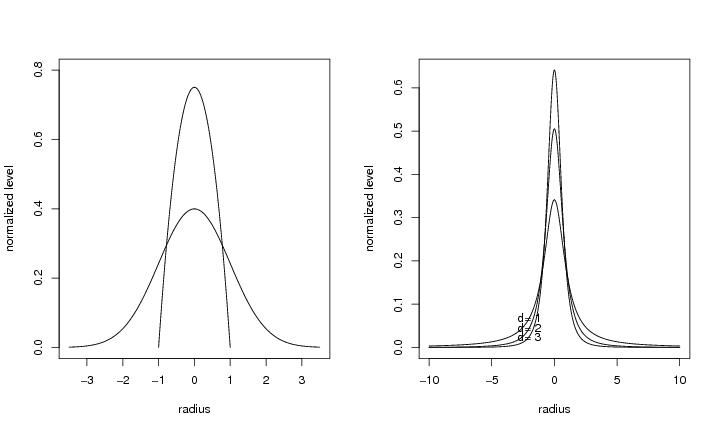
plotradi<-function(R,type,gnum=1000,sig=1,nu=1,d=d)
{
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=nu)
x<-rp$radi
y<-rp$levelnorma
sy<-symme(x,y)
xp<-sy$x
yp<-sy$y
plot(x=xp,y=yp,xlab="radius",ylab="normalized level",type="l")
}
plotmanyradi<-function(R,dimet,type,gnum=1000,sig=1,nu=1,inde=round(gnum/2))
{
xmax<-0
ymax<-0
for (i in 1:length(dimet)){
d<-dimet[i]
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=nu)
x<-rp$radi
y<-rp$levelnorma
xmax<-max(xmax,x)
ymax<-max(ymax,y)
}
plot(x="",y="",xlim=c(-xmax,xmax),ylim=c(0,ymax),
xlab="radius",ylab="normalized level")
for (i in 1:length(dimet)){
d<-dimet[i]
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=nu)
x<-rp$radi
y<-rp$levelnorma
sy<-symme(x,y)
xp<-sy$x-R
yp<-sy$y
matpoints(xp,yp,type="l",xlab="volume",ylab="level")
text(xp[inde],yp[inde],paste("d=",as.character(dimet[i])))
}
}
# frame 1
d<-1
type<-"bartlett"
R<-1
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=nu)
x<-rp$radi
y<-rp$levelnorma
sy<-symme(x,y)
xp<-sy$x-1
yp<-sy$y
type<-"gauss"
R<-3.5
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=nu)
x<-rp$radi
y<-rp$levelnorma
sy<-symme(x,y)
xp2<-sy$x-R
yp2<-sy$y
plot(x="",y="",xlim=c(-R,R),ylim=c(0,0.8),xlab="radius",ylab="normalized level")
matpoints(xp,yp,type="l",xlab="volume",ylab="level")
matpoints(xp2,yp2,type="l",xlab="volume",ylab="level")
# frame 2
type<-"student"
R<-10
dimet<-c(1:3)
nu<-1
plotmanyradi(R,dimet,type,nu=nu,inde=800)
Figure 24
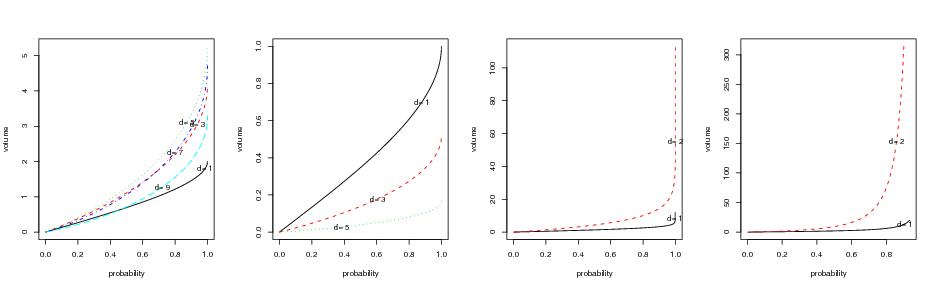
plotquantile<-function(R,dimet,type,gnum=1000,sig=1,nu=1,
inde=round(gnum/2))
{
coln<-length(dimet)
rown<-gnum
xm<-matrix(0,rown,coln)
ym<-matrix(0,rown,coln)
for (i in 1:length(dimet)){
d<-dimet[i]
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=1)
xm[,i]<-rp$proba
ym[,i]<-rp$volu
}
matplot(xm,ym,type="l",xlab="probability",ylab="volume")
for (i in 1:length(dimet))
text(xm[inde,i],ym[inde,i],paste("d=",as.character(dimet[i])))
}
# frame 1
type<-"bartlett"
gnum<-1000
R<-1
dimet<-c(1,3,5,7,9)
plotquantile(R,dimet,type,gnum=gnum,inde=900)
# frame 2
R<-0.5
sig<-0.5
dimet<-c(1,3,5)
plotquantile(R,dimet,type,gnum=gnum,sig=sig,inde=700)
# frame 3
type<-"gauss"
gnum<-1000
sig<-1
R<-6
dimet<-c(1:2)
plotquantile(R,dimet,type,gnum=gnum,inde=700)
# frame 4
type<-"student"
gnum<-1000
sig<-1
R<-10
nu<-1
dimet<-c(1:2)
plotquantile(R,dimet,type,gnum=gnum,inde=700,nu=nu)
Figure 25

plotquantile.norm<-function(R,dimet,type,gnum=1000,sig=1,nu=1,
inde=round(gnum/2),textdim=length(dimet))
{
coln<-length(dimet)
rown<-gnum
xm<-matrix(0,rown,coln)
ym<-matrix(0,rown,coln)
for (i in 1:length(dimet)){
d<-dimet[i]
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=nu)
xm[,i]<-rp$proba
ym[,i]<-rp$radi
}
matplot(xm,ym,type="l",xlab="probability",ylab="radius")
for (i in 1:textdim)
text(xm[inde,i],ym[inde,i],paste("d=",as.character(dimet[i])))
}
gnum<-1000
dimet<-c(1:20)
# frame 1
type<-"bartlett"
R<-1
plotquantile.norm(R,dimet,type,gnum=gnum,inde=700,textdim=5)
# frame 2
type<-"gauss"
R<-6
plotquantile.norm(R,dimet,type,gnum=gnum,inde=300,textdim=5)
# frame 3
type<-"student"
R<-20
nu<-1
plotquantile.norm(R,dimet,type,gnum=gnum,inde=300,textdim=5,nu=nu)
Figure 26
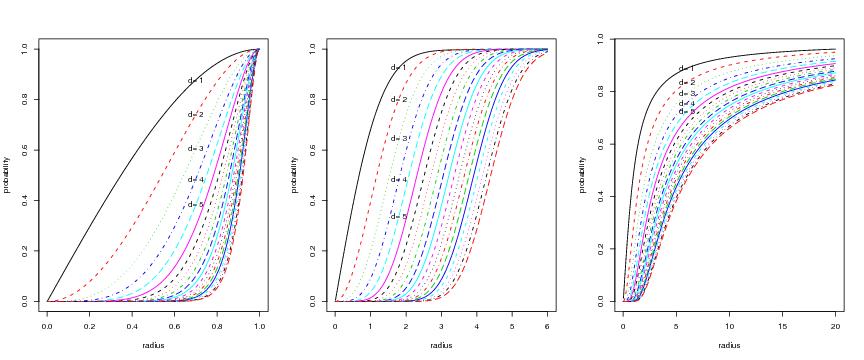
plotdistri.norm<-function(R,dimet,type,gnum=1000,sig=1,nu=nu,
inde=round(gnum/2),textdim=length(dimet))
{
coln<-length(dimet)
rown<-gnum
xm<-matrix(0,rown,coln)
ym<-matrix(0,rown,coln)
for (i in 1:length(dimet)){
d<-dimet[i]
rp<-tailfunc(R,d,type,gnum=gnum,sig=sig,nu=1)
xm[,i]<-rp$radi
ym[,i]<-rp$proba
}
matplot(xm,ym,type="l",ylab="probability",xlab="radius")
for (i in 1:textdim)
text(xm[inde,i],ym[inde,i],paste("d=",as.character(dimet[i])))
}
# frame 1
type<-"bartlett"
R<-1
plotdistri.norm(R,dimet,type,gnum=gnum,inde=700,textdim=5)
# frame 2
type<-"gauss"
R<-6
plotdistri.norm(R,dimet,type,gnum=gnum,inde=300,textdim=5)
# frame 3
type<-"student"
R<-20
nu<-1
plotdistri.norm(R,dimet,type,gnum=gnum,inde=300,textdim=5,nu=nu)
